What is Safety Analysis for Autonomous Systems?

You are in your car driving on the road. As you round a corner, you see a deer in the middle of the street. Will you be able to slam on your brakes and decelerate before you hit the deer? If not, will you be able to swerve out of the way safely? At what point are you doomed to crash? Could we make control systems in cars that ensure you will never be in a position where you are doomed to crash?

Safety analysis uses tools like Hamilton-Jacobi Reachability to find the mathematical answers to such questions. Let’s say I have some system that evolves over time (e.g. a car, a glucose monitor, an HVAC system in a house) and I can also define what would be unsafe for that system (e.g. hitting obstacles, allowing glucose to drop to dangerous levels, letting a house get too warm or too cold). Safety analysis claims to find the set of initial conditions from which your system will inevitably enter those unsafe conditions (e.g. when you are in a car at high speeds headed straight for an obstacle, and no matter how hard you brake or turn you are going too fast to prevent a crash). Once you know this reachable set of initial conditions that lead to unsafe states, you can work to ensure that your systems will never enter those inevitable conditions.

What is Hamilton-Jacobi (HJ) Reachability Analysis?

The Brief Explanation

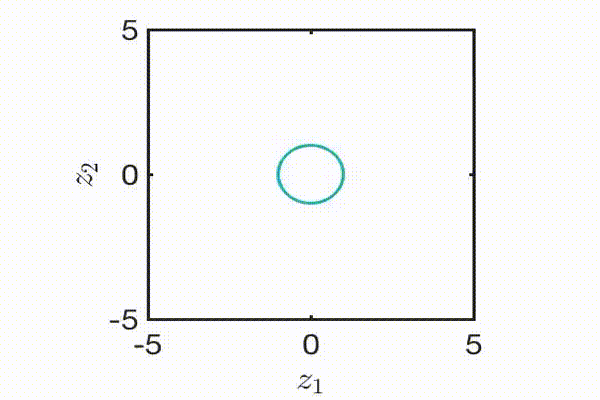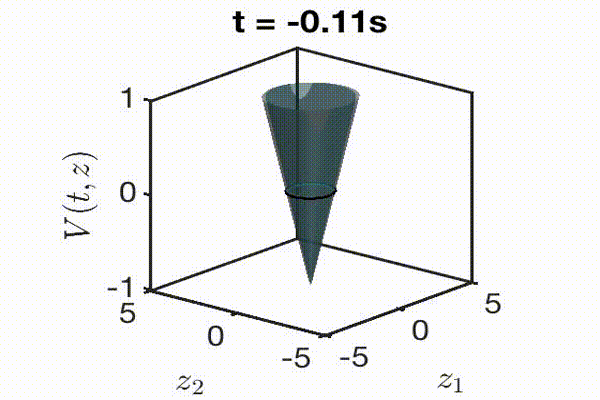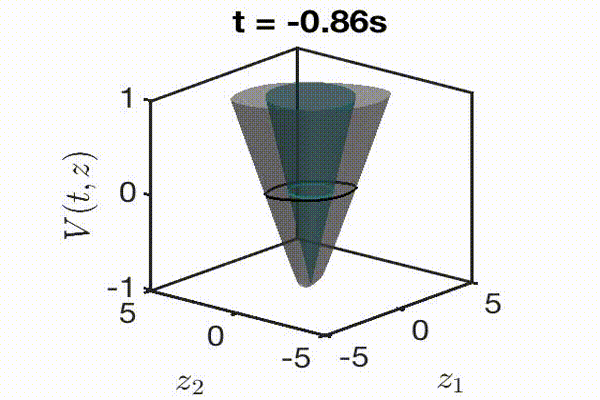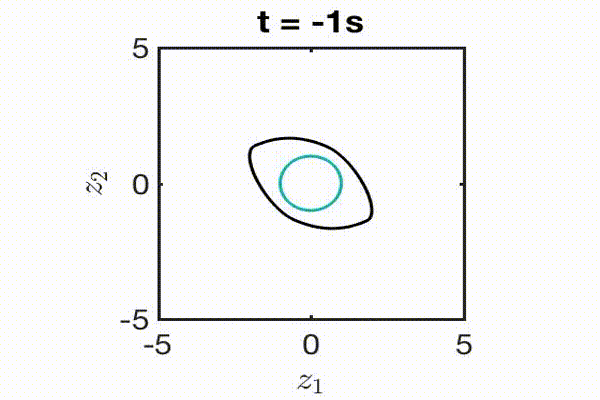
An animation of how we produce a reachable set. First the goal (or unsafe set) is defined, shown here as the blue circle. We then create a level set function that is a signed distance function: negative inside the set and positive outside. We propag… — An animation of how we produce a reachable set. First the goal (or unsafe set) is defined, shown here as the blue circle. We then create a level set function that is a signed distance function: negative inside the set and positive outside. We propagate this function using HJ reachability for the desired time horizon. Finally, we take the zero slice of this function to produce the reachable set

HJ reachability analysis is all about optimal control and guarantees for reaching goals and staying safe. When given a dynamic system and a goal, this method produces the set of initial states from which your system is guaranteed to reach that goal when using optimal control. What’s more, the method provides the optimal control to reach the goal. This can also be done for obstacles and unsafe states: HJ reachability will provide a set of initial states that your system must stay out of in order to remain safe, as well as the control to accomplish this. We can combine scenarios with both goals and obstacles, and we can even consider worst-case disturbances (e.g. wind).

The Thorough Explanation

Please see our tutorial paper for a more thorough introduction.

Why Study HJ Reachability?

Reachability analysis is extremely useful in safety-critical scenarios. When flying a plane or administering anesthetics, accidental mistakes from less rigorous planning methods can result in disaster. Reachability is able to provide guarantees on what is safe, as well as how to implement controls to accomplish your goal. What’s more, HJ Reachability can handle nonlinear dynamics and worst-case external disturbances.

The main challenge of HJ reachability lies in its expensive computational cost. Due to the nature of dynamic programming, the computational complexity of solving a reachability problem rises exponentially with the number of dimensions in the system. We have several works that tackle this problem from a control-theoretic perspective using tools like decomposition or reduced order models. We also have approaches that incorporate learning-based approaches that provide scalable approximations at high dimensions. These learning-based approximations can then be used by our more classical approaches to provide safety and goal-satisfaction guarantees.

Relevant papers

Learning-Based Approaches: Guide the learning process for physics-informed neural networks (PINNs) to obtain better safety assurances and control polices; Incorporate HJ reachability into reinforcement learning for improved safe RL [Students: Will Sharpless, Matthew Kim, Milan Ganai]
Refining Learned Solutions with Classical Methods: Given an approximate value function from learning-based approaches, we can globally or locally patch the solution to obtain guarantees. This can also be done online (for systems of up to ~5D) [Students: Sander Tonkens, Alex Toofanian]
Latent Linear Spaces: Learning or lifting to a linear latent space to solve an efficient linear game with conservative guarantees [Students: Will Sharpless, Nikhil Shinde]
Reduced-Order Modeling: Bounding the error in a reduced-order model with either classical approaches (e.g. dynamic programming or or sum-of-squares optimization) or learning-based approaches for fast online planning with safety and/or stability guarantees on the true model [Students: Zheng Gong, Boyang Li, Joe Jeong]
Decomposition: Decompose the system across space or time to obtain conservative results on the true solution [Students: Zheng Gong, Dylan Hirsch]

Available Toolboxes

helperOC (MATLAB) — Our public code for computing reachable sets can be cloned or downloaded at https://github.com/HJReachability/helperOC (note: this is essentially a user-friendly wrapper with extra functionality for Prof. Ian Mitchel’s level set toolbox). This MATLAB repository is the most user-friendly, and also contains a lot of visualization functionality. The downside is that it is not as efficient as the other toolboxes.
hj_reachability (Python) — this is the python implementation of the above toolboxes, lead by Edward Schmerling at Stanford. It is much more efficient than the MATLAB version and has an active group maintaining and updating it. It currently lacks some of the niche functionality of the helperOC toolbox, but is very good for most standard reachability applications and is adding new functionality rapidly.
DeepReach (Python) — Toolbox from Prof. Somil Bansal at the University of Southern California for approximating high-dimensional value functions using sinusoidal neural networks. Paper here.
BEACLS (C++) — BEACLS stands for Berkeley Efficient API in C++ for Level Set methods. It is essentially a reimplementation of the MATLAB toolboxes in C++ with tweaks to improve efficiency and compatibility with GPUs. It is quite a bit faster than the MATLAB implementation, but sacrifices readability for performance.
optimized_dp (Python/C++) — This toolbox was built by Prof. Mo Chen at Simon Fraser University, with the goal of having an easy python-based user interface to set up a reachability problem, and then conversion to fast C++ code via HeteroCL.
Flow* — Developed by Prof. Sriram Sankaranarayanan at CU Boulder. Good for computing safe sets for large numbers of states, and computing sets that do not have control/disturbance inputs (i.e. policy is already determined and plugged into dynamics). Uses scalability tools that lead to over-approximation of reachable sets.